STPM Math T Coursework 2015-2016 (Semester 3)
Question:
Hints:
Question 1a)
In order to select a random sample you need a list of all the students of your school. This list is called a sampling frame.
Suppose, for example, that the school consists of 450 upper secondary students and that you want to take a random sample of size 50. You would ....
Question 1b)
(I manage to get 50 girls' height (form 4 and form 5) from my tuition centre together with their parents' height.)
Question 2
-Study chapter 16 for confidence interval for the mean height of the students under subtopic population with unknown varance, large sample
Question 3a)
- Use the formula given above to count the predicted height. (Use Microsoft Excel)
Question 3b)
- Find range, divide into 3 equal class widths to get 3 categories
Question 4(a)
-Study chapter 18: Goodness of fit Test
Question 4(b) & (c)
- no hint.
(I manage to get 50 girls' height (form 4 and form 5) from my tuition centre together with their parents' height.)
Question 2
-Study chapter 16 for confidence interval for the mean height of the students under subtopic population with unknown varance, large sample
Question 3a)
- Use the formula given above to count the predicted height. (Use Microsoft Excel)
Question 3b)
- Find range, divide into 3 equal class widths to get 3 categories
Question 4(a)
-Study chapter 18: Goodness of fit Test
Question 4(b) & (c)
- no hint.
Full solution
Full solution is ready. It includes Introduction (1 page), Methodology (2 pages), Results for question 1 to 4 (5 handwritten pages and 5 pages in Microsoft Excel format) , and Conclusion (2 pages)
** The full solution is the sample answer for students reference**
1) Bank in RM40 to CIMB bank account: 8600470918, Account name: Pusat Tuisyen Teman Pintar.
2) SMS/Whatapps your payment receipt/transaction slip to 0163551988. Let us know your contact number as well.
3) We will email the full solution to you within 2 days and text you once the email is sent.
STPM Math T Coursework 2015-2016 (Semester 2)
Question:
Hints:
Question 1a) Use Area of triangle = 1/2 r (square) sin theta
Question 1b) n/2 x (square) sin (...)
Question 1c) 3.142
Question 2a)i) e ii) e to the power of k (May use Microsoft excel)
2b) Manage to find out 2 methods to show this. Method 1: substitution method (short method). Method 2: tabulation method (long method)
Question 3: Trapezium rule is a subtopic in the last chapter in semester 2: Numerical method
3 (a) i) 3/4
ii) 17/24
iii) 1171/1680
3 (b) ln (2t/t+1), ln 2.
3 (c) -
3 (a) i) 3/4
ii) 17/24
iii) 1171/1680
3 (b) ln (2t/t+1), ln 2.
3 (c) -
Full solution
1. Results (8 pages of hand-written solution and 2 pages of microsoft excel tables),
2. Methodology (4 pages) and
3. Conclusion (3 pages).
2. Methodology (4 pages) and
3. Conclusion (3 pages).
To get the full solutions for results,methodology and conclusion, you can buy it from us . Just follow the following steps:
1) Bank in RM40 to CIMB bank account: 8600470918, Account name: Pusat Tuisyen Teman Pintar.
2) SMS/Whatapps your payment receipt/transaction slip to 0163551988. Let us know your contact number as well.
3) We will email the full solution to you within 2 days and text you once the email is sent.
Introduction?
Hints:
For question 1, check for how the formula of area of circle is being developed.
For question 2, check for the usage of limits
For question 3, find out how trapezium rule formula is obtained.
STPM Math T Coursework 2015-2016 (Semester 1)
Question:
Parametric equations express a set of related quantities as explicit functions of an independent variable, known as a parameter. An equation, relating variables  and
and 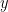 in Cartesian coordinates, can be expressed by parametric equations which describe a position on the curve.
in Cartesian coordinates, can be expressed by parametric equations which describe a position on the curve.
1 The parametric equations of a plane curve are defined by  .
.
Tabulate the values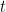 ,
,  and
and 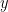 , and plot the curve.
, and plot the curve.
Tabulate the values
2 (a) Find three sets of parametric equations for the curve whose equation is %5E2+%3D+x+-+49&bg=ffffff&fg=000&s=0) .
.
(b) Is it possible to choose as the parametric equation for
as the parametric equation for  ? Can you start with any choice for the parametric equation for
? Can you start with any choice for the parametric equation for  ?
?
(c) Can you start with any choice for the parametric equation for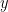 ?
?
(b) Is it possible to choose
(c) Can you start with any choice for the parametric equation for
3 Suppose that the position of a particle at time 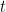 is given by
is given by
and the position of another particle is given by
(a) Sketch the paths of the particles on the same coordinate axes.
(b) How many points of intersection are there?
(c) Determine whether there is any point where the particles collide.
(b) How many points of intersection are there?
(c) Determine whether there is any point where the particles collide.
Solution:
1.
2.a)
Method 1:
To get the full solutions for the whole calculation part, you can buy it from us . Just follow the following steps:
1) Bank in RM30 to CIMB bank account: 8600470918, Account name: Pusat Tuisyen Teman Pintar.
2) SMS/Whatapps your payment receipt/transaction slip to 0163551988. Let us know your contact number as well.







Can i ask ? what the thing must have in math T coursework term 2. Accept intro , meto , result and conclusion .Thank you
ReplyDeletethat's all for the assignment
ReplyDeletecan I get the intro for term 2 2016
ReplyDeleteI am very impress on your information ,Its a really very impressive blog. I really got some another very nice information , so thanks for sharing these tips.
ReplyDeleteIp Tuition Singapore
Intro, methodology, results and conclusion
ReplyDelete